
Vladimir Sobes
Neutrons in a reactor may move at a variety of speeds, but it’s the slow-moving ones that have the highest probability of creating fission. The quantification of this probability, known as a cross-section, is important for nuclear reactor engineers to be able to increase the incidence of fission.
NE Assistant Professor Vladimir Sobes and MIT PhD student Pablo Ducru, along with other collaborators at MIT, have recently demonstrated a new formula that streamlines the calculations of cross-sections and adds rigor to the results.
His research, which took seven years to complete, was recently published in Physical Review C. The contribution to science could change the whole industry’s approach to cross-section modeling.
“It was a great pleasure to work with Pablo and our other collaborators at MIT,” said Sobes.
Nuclear reactor engineers purposefully slow down neutrons in a reactor with hydrogenous materials such as water or graphite to get them to the speed at which they are likely to cause fission. A fission event then creates more fast-moving neutrons that will need to be slowed down again. Thus, the neutrons that create fission energy in a nuclear reactor travel in a closed loop.
To keep this loop producing the right amount of energy, engineers need to be able to predict the behavior of nuclear reactors, which depends on knowing the probability that a neutron will create fission as a function of the kinetic energy. This requires computer simulations that use collected cross-section data, or every known incident of a neutron hitting another atom.
This data is stored in vast digital libraries managed by international communities, such as the US’s database at the Evaluated Nuclear Data File at the National Nuclear Data Center at Brookhaven National Lab.
The research purpose was to seek the best formula that would accelerate the simulation of the nuclear reactors. Sobes’s and Durcu’s contribution is a mathematically optimal way to store the cross-section information.
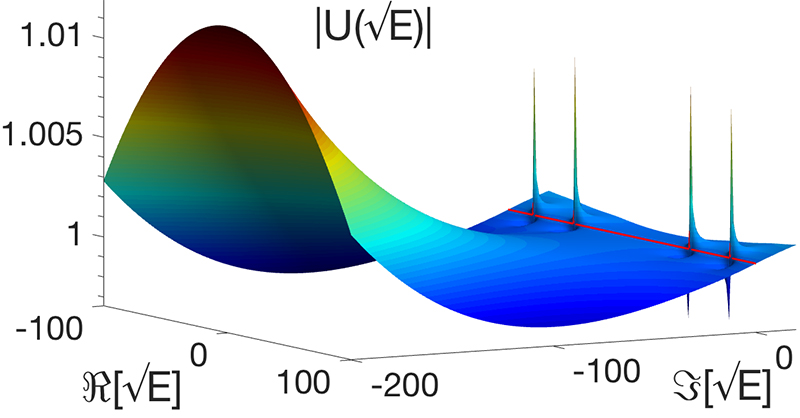
The key to the new formula was to expand the mathematical equations into the complex plane, which not only includes real numbers, such as 1.00, 2.35, 7.84, but also imaginary numbers, such as 3.74i, where, i=√(-1). This actually simplifies the equations and shows how everything depends only on the location and size of the poles (spikes) in the complex plane. Five poles are visible in the figure above, four sharp poles and one wide pole on the left side of the figure. The key information for nuclear engineering lives only on one line (red line) in the complex plane.
Compared to the current industry-standard, the Wigner-Eisenberg parameters, the new results are unambiguous. Changing the format for how cross-section information is stored for the future, creates a universal standard formula, similar to how the Kelvin scale of temperature is a universal standard that reduces ambiguities between Celsius and Fahrenheit.